AC-CVXPY: Automatic Hardware Solvers Design for Robotics and Finance
Emerging Applications of Convex Optimization
Convex optimization is essential in various performance-critical applications, including machine learning, finance, control engineering, power systems, and signal processing. As the complexity and scale of these problems grow, there is an urgent need to significantly enhance the performance and efficiency of convex program solvers.
Innovation
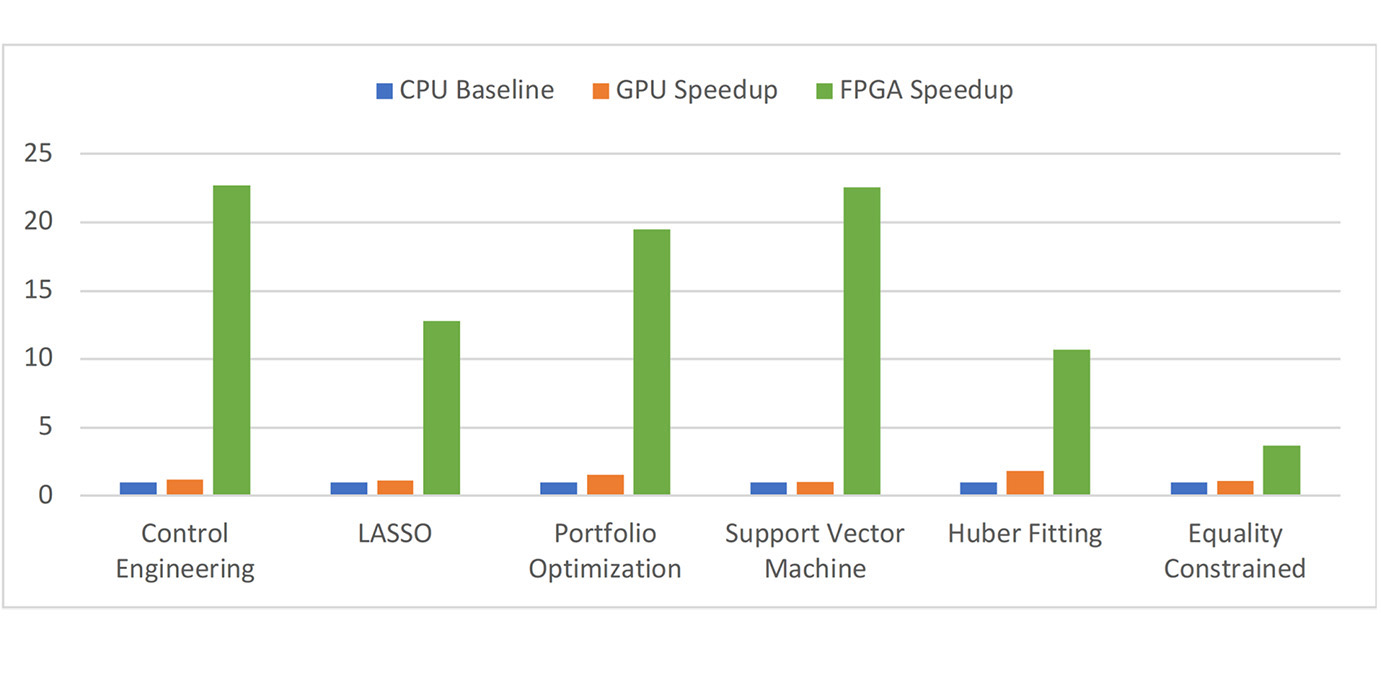
We present an automated algorithm-hardware co-design framework called AC-CVXPY, designed to boost the speed and power efficiency of solvers for convex optimization while maintaining solution accuracy. This framework automatically creates dedicated and efficient hardware implementations for any convex optimization problem, tailored to specific requirements for latency, power budget, and hardware resource utilization. Preliminary FPGA prototypes demonstrate a geometric mean speedup of 30.5x and 127.0x greater energy efficiency compared to the same solver algorithm on a comparable CPU backend across 100 QP problems from five application domains.
Low-latency Arbitrages Trading System Demonstration
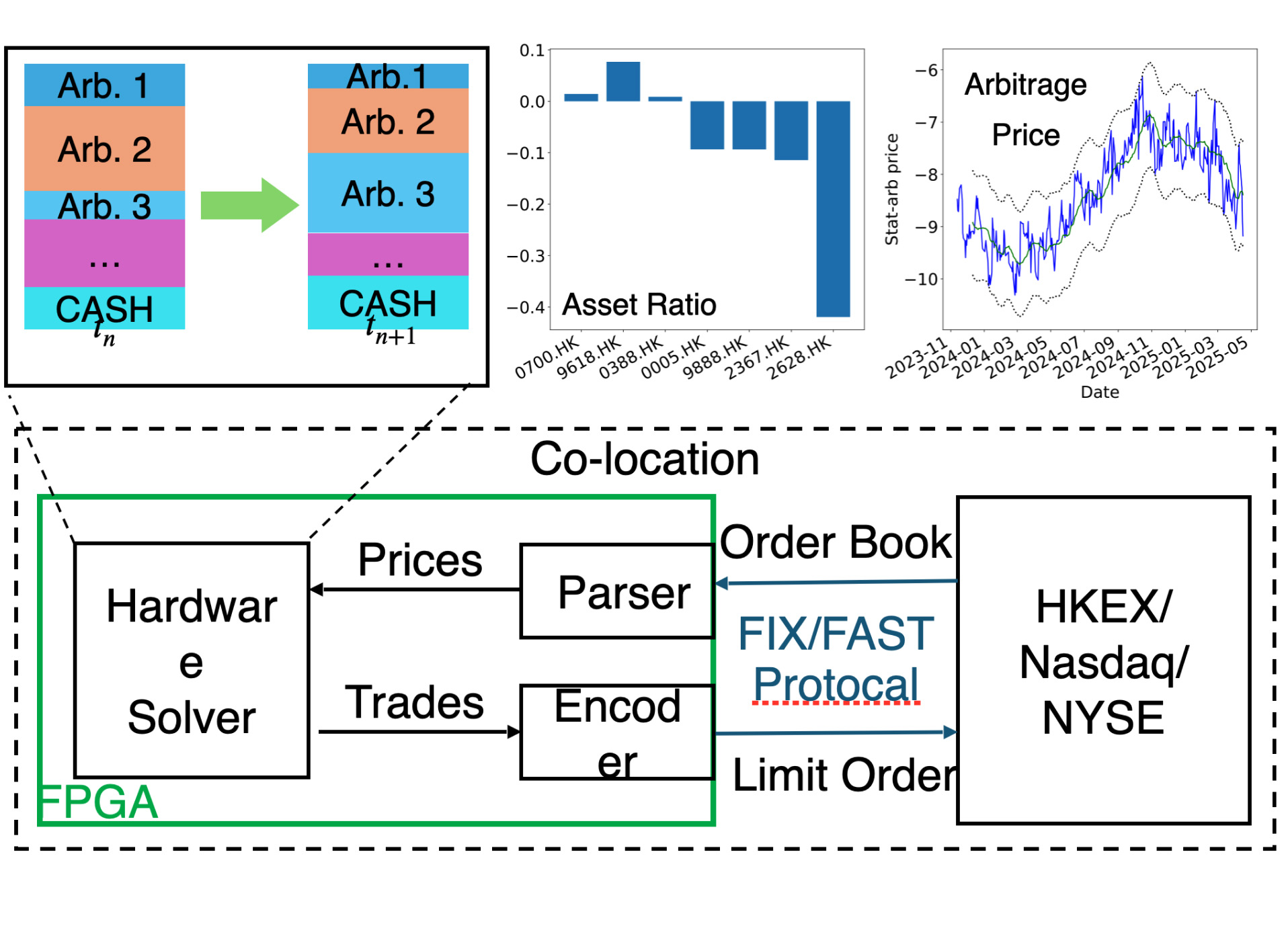
Portfolio optimization is a crucial challenge in financial computing. General-purpose computing platforms often fail to meet the low-latency computational needs for optimizing portfolio trading strategies. We have developed a prototype trading system based on AC-CVXPY, capable of efficiently executing low-latency portfolio trading through statistical arbitrage.
Low-latency and Energy-efficient Controller Demonstration

Model Predictive Control (MPC) is a powerful control framework, yet its stringent performance requirements for computational infrastructure limit its widespread use in various scenarios. We have developed a controller prototype based on AC-CVXPY, which can be deployed on ultralightweight drones like the 27g Crazyflie. The controller can run a state-of-the-art MPC solver algorithm with a 10x latency reduction compared to MCU-based solutions, under the same power and area constraints.
